Least-square Solution

• Least-square Solution은 다양한 분야에서 사용되는 데이터 기반의 근사화 기법이다.

1. Pseudo-inverse Maxtrix

Matrix Equation에서의 Least-square Solution은 다음과 같이 유도된다.
구하고자 하는 벡터 \(x\)가 다음 Matrix equation을 만족할 때,

$$Ax=b\ \ \ \ \ \ \ \cdots\ \ \ \rm{(1)}$$

행렬 \(A\)가 정방행렬이 아니라면, \(A\)의 역행렬이 존재하지 않기 때문에 아래와 같은 수식을 쓸 수 없다.

$$x=A^{-1}b$$

그런데, 식 (1)에서 양번에 \(A^{T}\)를 왼쪽에 곱하면 다음과 같이 되며,

$$A^{T}Ax=A^{T}b$$

여기에서, \(A^{T}A\) 는 정방행렬이 된다.
\(A\)가 영행렬이 아니라면, 자기 자신의 전위행렬을 곱한 정방행렬은 Non-singular Matrix이므로 다음과 같이 \(x\)를 구할 수 있다.

$$x=(A^{T}A)^{-1}A^{T}b$$

2. Pseudo-inverse Solution 예시

2.1. 1차 선형 근사화

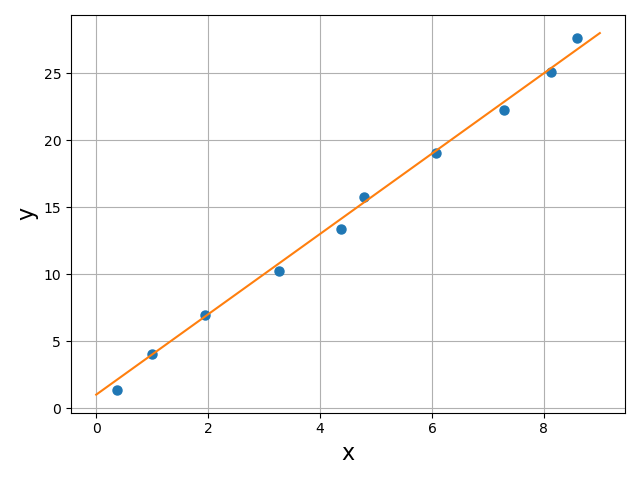
이론 상 1차 선형인 시스템에서 점 데이터 \((x, y)\)를 \(N\)개 얻었다고 가정하자.
이 때, 이 데이터를 대표할 수 있는, 오차가 가장 작은 1차 방정식 \(y=ax+b\) 의 계수 \(a\)와 \(b\)를 구하고자 한다.

\(N\)개의 데이터 \((x_{1},\ y_{1}),\ (x_{2},\ y_{2})\ \cdots ,\ (x_{N},\ y_{N})\)는 이론적으로 다음을 만족한다.

\[y_{1}=ax_{1}+b \\ y_{2}=ax_{2}+b \\ \vdots \\ y_{N}=ax_{N}+b\]

이것을 행렬 방적식으로 표현하면, 다음과 같다.

\[\begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \end{bmatrix}= \begin{bmatrix} x_{1} & 1 \\ x_{2} & 1 \\ \vdots & \vdots \\ x_{N} & 1 \\ \end{bmatrix} \begin{bmatrix} a \\ b \end{bmatrix}\]

여기에서, \(\begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \end{bmatrix}\) 를 \(y\), \(\begin{bmatrix} x_{1} & 1 \\ x_{2} & 1 \\ \vdots & \vdots \\ x_{N} & 1 \\ \end{bmatrix}\)를 \(X\)라고 하고 다음과 같이 간단히 표현할 수 있다.

\[y=X \begin{bmatrix} a \\ b \end{bmatrix}\]

Pseudo-inverse Matrix를 이용하면 다음과 같이 \(a\)와 \(b\)를 구할 수 있다.

\[\begin{bmatrix} a \\ b \end{bmatrix}=(X^{T}X)^{-1}X^{T}\]

2.2. 원 근사화

이번에는 원의 방정식을 만족해야 하는 데이터를 얻었다고 가정하자.

\((x-a)^{2}+(y-b)^{2}=r^{2} \\ (x^{2}-2ax+a^{2})+(y^{2}-2by+b^{2})=r^{2} \\ x^{2}+y^{2}=2ax+2by+(r^{2}-a^{2}-b^{2})\)
\(r^{2}-a^{2}-b^{2}=c\) 로 치환

\(x^{2}+y^{2}=2ax+2by+c\)
데이터 \((x_{1},\ y_{1}),\ (x_{2},\ y_{2})\ \cdots ,\ (x_{N},\ y_{N})\)에 대해서 식을 정리하면,

\[x_{1}^{2}+y_{1}^{2}=2ax_{1}+2by_{1}+c \\ x_{2}^{2}+y_{2}^{2}=2ax_{2}+2by_{2}+c \\ \vdots \\ x_{N}^{2}+y_{N}^{2}=2ax_{N}+2by_{N}+c\]

행렬로 표현하면 다음과 같다.

\[\begin{bmatrix} x_{1}^{2}+y_{1}^{2} \\ x_{2}^{2}+y_{2}^{2} \\ \vdots \\ x_{N}^{2}+y_{N}^{2} \end{bmatrix}= \begin{bmatrix} 2x_{1} & 2y_{1} & 1 \\ 2x_{2} & 2y_{2} & 1 \\ \vdots \\ 2x_{N} & 2y_{N} & 1 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \end{bmatrix}\]

Pseudo-inverse를 사용하여 \([a\ b\ c]^{T}\)를 구할 수 있다.

\[\begin{bmatrix} a \\ b \\ c \end{bmatrix}= \left( \begin{bmatrix} 2x_{1} & 2y_{1} & 1 \\ 2x_{2} & 2y_{2} & 1 \\ \vdots \\ 2x_{N} & 2y_{N} & 1 \end{bmatrix}^{T} \begin{bmatrix} 2x_{1} & 2y_{1} & 1 \\ 2x_{2} & 2y_{2} & 1 \\ \vdots \\ 2x_{N} & 2y_{N} & 1 \end{bmatrix} \right)^{-1} \begin{bmatrix} 2x_{1} & 2y_{1} & 1 \\ 2x_{2} & 2y_{2} & 1 \\ \vdots \\ 2x_{N} & 2y_{N} & 1 \end{bmatrix}^{T} \begin{bmatrix} x_{1}^{2}+y_{1}^{2} \\ x_{2}^{2}+y_{2}^{2} \\ \vdots \\ x_{N}^{2}+y_{N}^{2} \end{bmatrix}\]

원의 반지름 \(r\)은 \(r=\sqrt{c+a^{2}+b^{2}}\) 으로 구할 수 있다.